Quantum entanglement
Entanglement entropy provides a quantum information perspective to understand the long-distance properties of correlated many-body state and can be used to classify strongly correlated phases of matter in and out of equilibrium.
We study the entanglement scaling of 2+1 dimensional critical systems. Our main results include:
- The universal subleading correction term of entanglement entropy of various 2+1 dimensional critical system defined on spatial torus.
- The entanglement entropy and mutual information of quantum Lifshitz model.
- The entanglement Aharonov-Bohm effect for critical system. This method is further used to detect the low energy excitation of spin liquid on Kagome lattice.
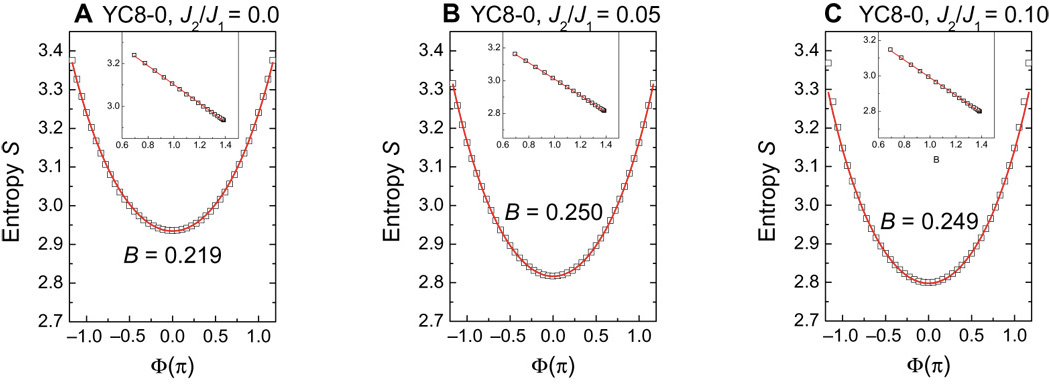
- We explore the entanglement scaling of one classical of one dimensional critical wave function which is the ground state of quantum spin chain model with dynamical exponent z>1.